Automorphism Group Computation
in traces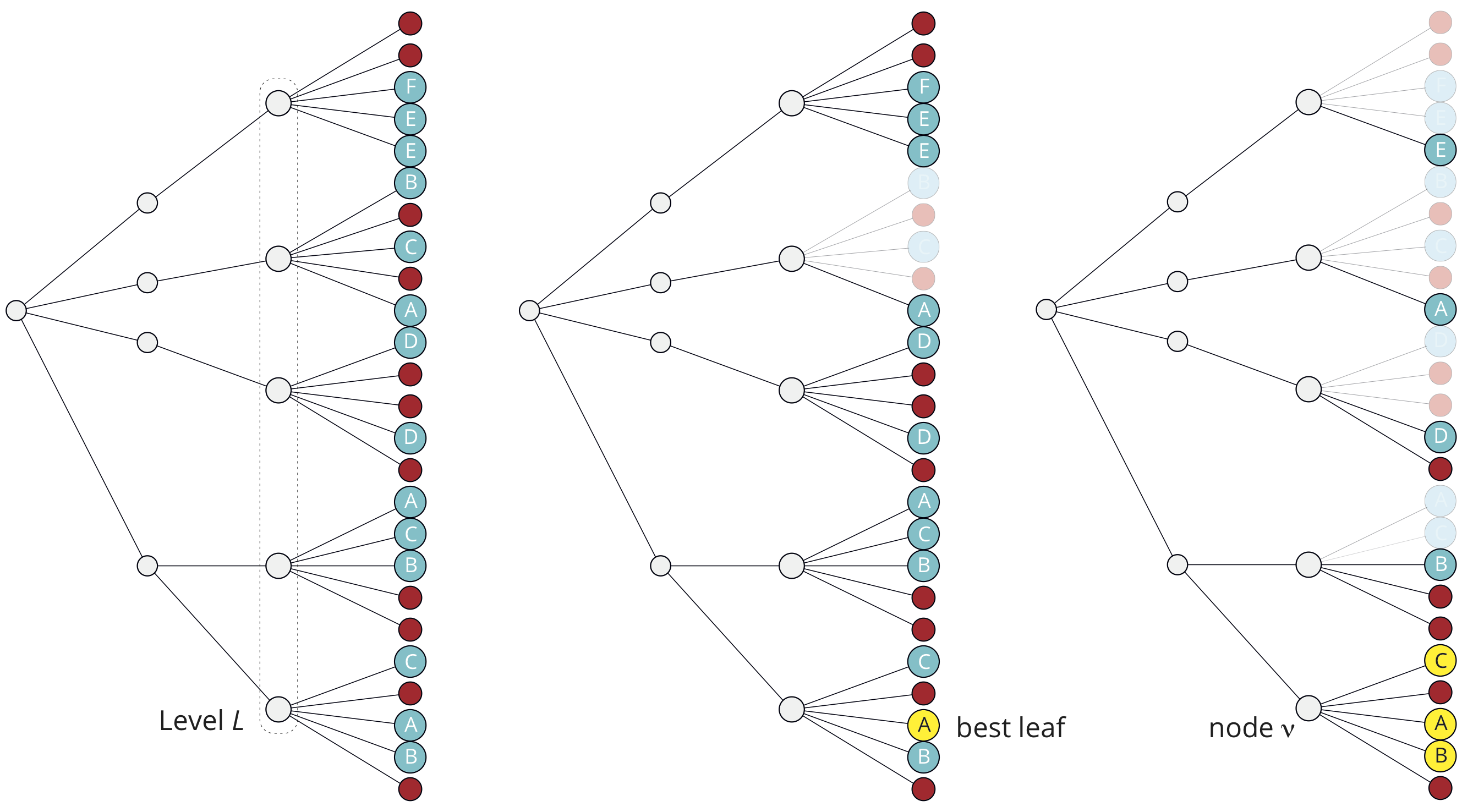
When Traces is only looking for the automorphism group, and not for a canonical labelling, it employs a strategy which is sometimes much faster than the basic one. Suppose that while generating the nodes on some level L, it notices (during experimental path generation) that one of them, say ν, has a child which is discrete. At this point, Traces determines and keeps all the discrete children of ν (modulo the usual automorphism pruning). Now, for all nodes ν' on level L, a single discrete child is found, if any, and an automorphism is discovered if it is equivalent to any child of ν. The figure shows (left) the whole tree up to level L+1, where a node labelled by X represents a discrete partition with certificate X, while an unlabelled (red) node stands for a non-discrete partition. The tree at the center of this figure shows the part of the tree which is traversed by Traces during the search for a canonical labelling. Only the best leaf is kept for comparison with subsequent discrete partitions. The tree at the right side of the figure shows the part of the tree which is traversed by Traces during the automorphism group computation. All the discrete children of ν are kept for comparison with subsequent discrete partitions. When the first discrete partition is found as a child of a node ν' at level L, either it has the same certificate as one of the stored ones, or the whole subtree rooted at ν' has no leaf with one of such certificates. In the first case, an automorphism is found. In both cases, the computation is resumed from the next node at level L.